Люди, делающие ставки, часто поглощены мыслями об успехе. Они хотят как можно меньше проиграть и как можно больше выиграть. Эндрю Мэк (Andrew Mack), создатель статистической модели для спортивных соревнований в Excel, убежден: секретом достижения успеха может быть неудача. В своей статье он объясняет, почему.
Неудача: секрет успеха в ставках на НХЛ?
В моделировании для спортивных соревнований неудачи могут постепенно привести к успеху. В этой статье автор поделился простым методом расчета вероятностей для результата 1X2 на примере игры НХЛ. Для начала рассмотрим базовый шаблон модели, который вы можете сами без труда использовать в Excel. Модель простая, но функциональная.
В данную модель стоит вникнуть, чтобы обратить внимание на некоторые элементы моделирования в спорте, которые редко обсуждаются: неудача, критический анализ с помощью знаний в конкретной области и исправление недостатков.
Вы можете удивиться, но в создании моделей зачастую учишься именно на неудачах, а не на успехах. Когда мы рассмотрим эту модель и установим базовый процесс, мы критически проанализируем ее недостатки, чтобы понять, можем ли мы что-то улучшить. Я надеюсь предложить вам кое-что более ценное в долгосрочной перспективе, чем просто модель. Речь идет о процессе исправления ошибок, который позволим вам оттачивать собственные идеи, до тех пор пока они не будут приносить желаемые результаты. Приступим!
Шаг 1. Соберите данные статистики
Для начала нам потребуется информация. Давайте перейдем на сайт Hockey-Reference и скопируем в таблицу Excel результаты всех матчей сезона НХЛ 2019–2020.
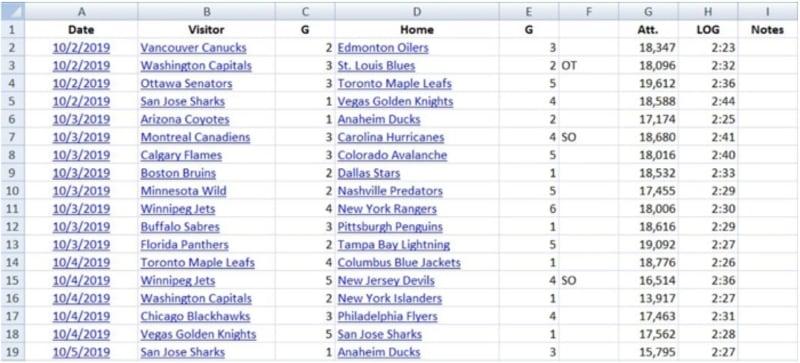
Из одних только этих данных мы можем извлечь ценную информацию. Допустим, нам нужно узнать среднее количество шайб, заброшенных хозяевами и гостями, отклонение для заброшенных шайб или как часто игрались овертаймы.
Если мы воспользуемся функциями AVG и VAR в Excel, мы увидим, что хозяева забрасывают в среднем 3,3 шайбы за игру, а гости — 2,85. Отклонение составляет соответственно 2,85 и 2,62. На долю овертаймов в этом сезоне приходится примерно 26,81 % от общей продолжительности сыгранных матчей. Итак, у нас есть данные. Теперь выполним распределение по нашему целевому результату.

Шаг 2. Создайте распределение по целевому результату
Предположим, что нашим целевым результатом является количество шайб, заброшенных каждой командой. Этот показатель поможет нам спрогнозировать, кто победит и как часто будет побеждать команда. Полезно было бы знать, к какому типу статистического распределения относятся эти данные. Эта информация поможет нам на этапе конвертирования ожиданий в вероятности.
Мы знаем, что количество забитых шайб в НХЛ — это дискретные счетные данные. Существует множество вариантов забросить шайбу, Лучшим выбором будет распределение Пуассона. Можно убедиться в этом с помощью любых надстроек для Excel:
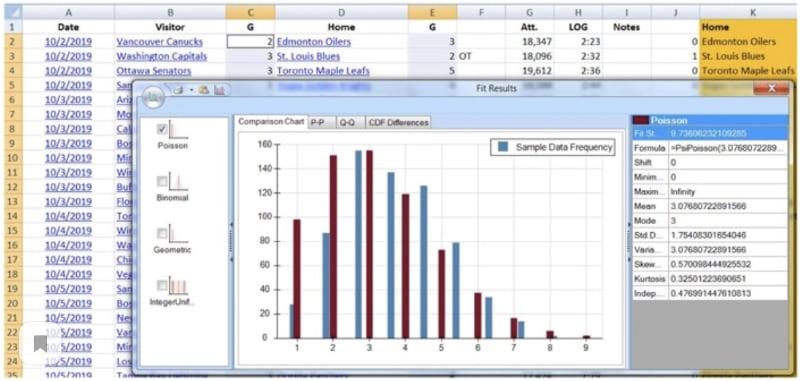
Распределение Пуассона отлично подходит для наших данных. И это неудивительно, поскольку данная методика тщательно тестировалась в течение многих лет различными исследователями. Оставим пока информацию о распределении в уме и продолжим. Скоро она нам понадобится.
Шаг 3. Скорректируйте прогноз для каждой команды с учетом оппонента
У нас есть данные, целевой результат и распределение вероятностей. Теперь нам нужна структура модели для составления базового прогноза на каждую игру. Для этого примера будем использовать простую структуру, которая учитывает среднее количество заброшенных шайб за и против каждой команды дома и в гостях, а также общее среднее количество заброшенных шайб. Функция будет выглядеть так:
Количество шайб за команду = (Среднее количество шайб за команду + Среднее количество шайб против оппонента)/2
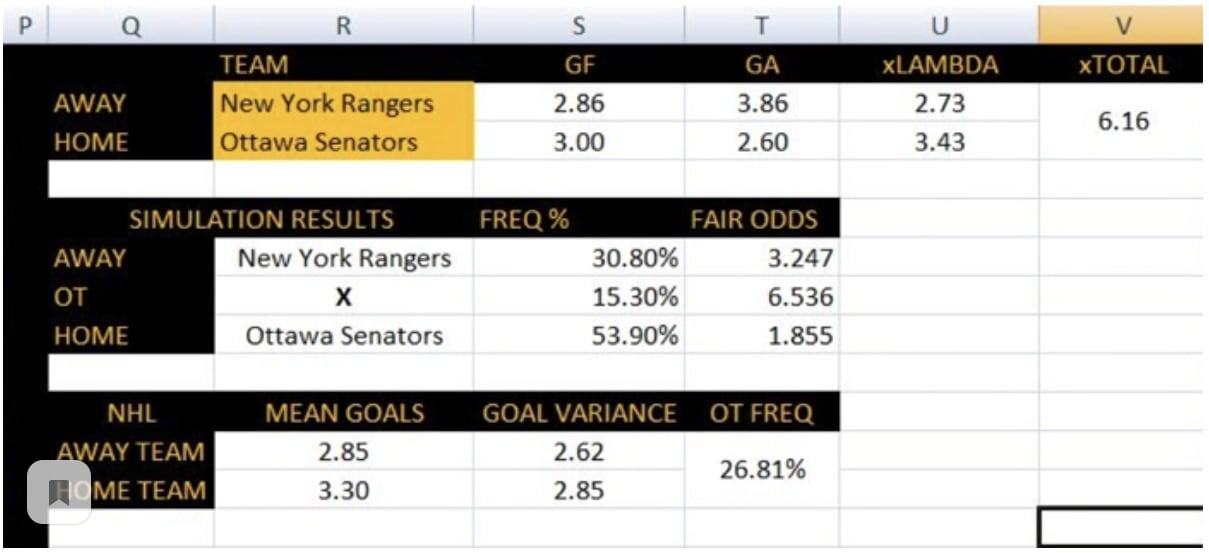
Таким образом мы учитываем и нападение, и оборону, и преимущество домашнего льда (хотя и в упрощенном виде). Попробуем воспользоваться нашей моделью на примере матча «Нью-Йорк Рейнджерс» и «Оттава Сенаторс», который был сыгран 22 ноября. Наш прогноз: «Оттава» забросит 3,43 шайбы, а «Нью-Йорк» — 2,73. Таким образом, наша модель отдает победу «Оттаве».

Шаг 4. Выполните моделирование результатов, чтобы учесть фактор случайности
Теперь, когда у нас есть ожидания относительно заброшенных шайб для обеих команд, нужно конвертировать эти ожидания в вероятности. Можно воспользоваться матрицей Пуассона, о которой я писал в книге «Статистические модели в Excel для спортивных соревнований». Это нетрудно сделать в Excel с помощью функции ПУАССОН.
Недостаток этого метода заключается в том, что он не учитывает фактор случайности. Чтобы получить более надежный прогноз на исход матча, мы попробуем использовать моделирование пуассоновского процесса. Воспользуемся функцией генерации случайных чисел в Excel.
Предположим, что в вашей версии Excel есть набор инструментов анализа данных. Нажмите «Данные», затем «Анализ данных» и выберите «Генерация случайных чисел».
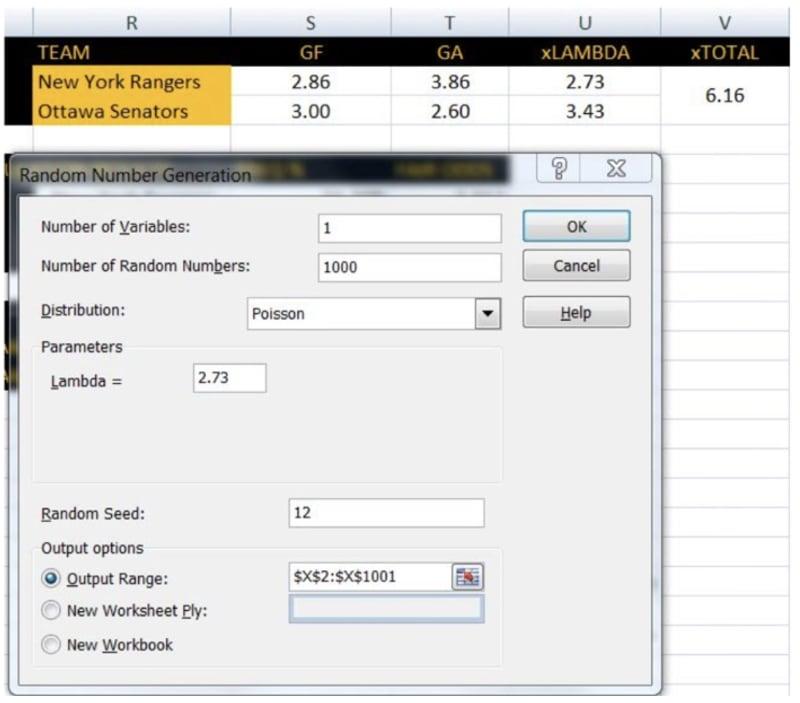
Мы смоделируем 1000 игр с использованием наших ожиданий для каждой команды. Затем мы сможем вычислить частоту, с которой выигрывает каждая команда, частоту овертаймов и т. д.
Давайте введем «1» для количества переменных, «1000» для количества случайных чисел (количество смоделированных игр), в качестве метода распределения выберем «Пуассона» и укажем количество ожидаемых заброшенных шайб для «Нью-Йорк Рейнджерс» (2,73) в качестве лямбды. Когда мы выберем место в таблице, где должны отображаться результаты, нажмем «ОК».
По завершении моделирования проделаем всё то же самое для «Оттавы», убедившись в том, что результаты будут отображаться в соседнем столбце на листе.
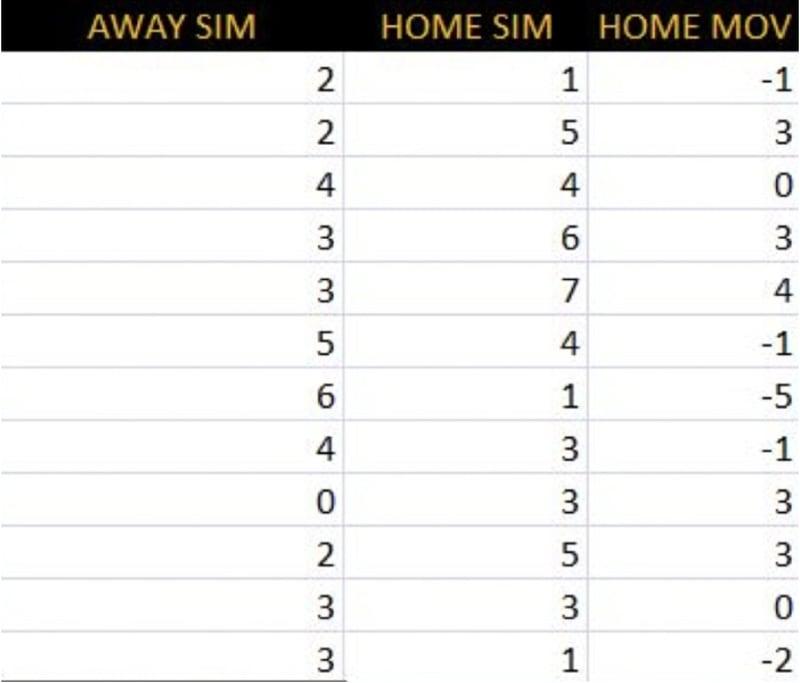
Шаг 5. Конвертируйте ожидания в вероятности
Теперь, когда моделирование для обеих команд выполнено, нам нужно определить вероятность победы хозяев, победы гостей и ничьи в основное время. Добавим на наш лист столбец с результатом хозяев [MOV]. Затем посчитаем, сколько раз из 1000 результат хозяев будет больше нуля, меньше нуля и равен нулю.
Тем самым мы сможем вычислить коэффициенты на победу хозяев, победу гостей и на ничью в основное время. Наша модель позволяет получить следующие коэффициенты: на победу «Нью-Йорка» — 3,247, на победу Оттавы — 1,855 и на ничью в основное время — 6,536. Затем мы можем сравнить эти коэффициенты с рыночными, чтобы найти переоцененные коэффициенты и сделать ставку с перевесом.
Анализ слабых мест модели
«Оттава» выиграла в этом матче в основное время. Но не стоит думать, что у нас в руках теперь есть беспроигрышная модель. Несмотря на разовый успех, эта модель далека от совершенства. Пожалуй, еще, не стоит делать ставки с ее помощью. Использовать ее против рынка — это всё равно что ввязываться с ножницами в перестрелку. Это вполне очевидно. Вы тоже убедитесь в этом, если протестируете данную модель на ретроспективных данных.
Не столь очевидным может быть другое, особенно если вы новичок в моделировании: почему же данная модель несостоятельна. На этом этапе разработчик модели может испытать разочарование. Вы проделали немало работы, создали, как вам казалось, эффективный процесс и потерпели неудачу. Вы потратили немало времени и сил, а теперь вынуждены начинать все с нуля.
Но не стоит окончательно списывать модель со счетов. Наоборот, с этого момента начинается настоящая работа.
Хорошую модель можно сравнить с качественным биноклем. Он позволяет детально рассмотреть объекты, которые находятся на большом расстоянии. Плохие модели не позволяют смотреть вдаль (или, что еще хуже, смотрят назад!) и не отличаются высоким «разрешением». Плохой результат при проведении ретроспективного теста является индикатором того, что наша модель не способна дать «четкую картину» будущих событий. Когда это происходит, нужно спросить себя:
Какие отклонения в фундаментальном процессе мы упустили из виду? Какие мы сделали допущения, которые оказались катастрофическими? Как добиться более «четкой картинки»? Ниже вы увидите несколько рекомендаций, как исправить недостатки. Попробуйте улучшить свою модель с учетом ее недостатков. В конце концов, вы можете превратить ее в ценный и надежный инструмент для составления прогнозов.
Исходные статистические данные для прогнозирования
Пришло время разобрать эту модель на части, чтобы понять, где мы ошиблись. Начнем с исходных данных. Казалось, всё просто: мы хотели спрогнозировать количество заброшенных шайб, поэтому использовали показатель «заброшенные шайбы». Вроде бы правильно.
Но тут есть свои нюансы. Данные о заброшенных шайбах — это данные о результате. Результаты в спорте всегда содержат элемент шума, потому что некоторая доля результатов не определяется воспроизводимыми движениями и приемами, которые мы можем точно спрогнозировать.
Чем случайнее результат в спорте, тем больше статистический шум. Для хоккея это вполне справедливое утверждение. Мы не смоделировали шум, и это одна из причин, почему наша модель показала плохие результаты.
Что мы видим в хоккейных матчах: шайбы, заброшенные в пустые ворота, рикошеты или ситуации, когда игрок подправляет локтем шайбу, летящую после дальнего броска, и она попадает в ворота. Во всех этих случаях регистрируются заброшенные шайбы. Следует ли считать такие моменты проявлением превосходства одной команды над другой? Скорее всего, нет. Здесь особую важность приобретают такие методы статистического анализа, как регрессионное моделирование. А показатель ожидаемого количества заброшенных шайб является более надежным предиктором будущего успеха, чем количество фактически заброшенных шайб.
Когда вы отсекаете как можно больше шума, вы можете точнее сопоставить воспроизводимые движения или приемы, которые приводят к голу. Таким образом, отнесение фактически заброшенных шайб на счет способностей команды в любом сценарии, где много шума, является ошибкой. Если мы будем понимать и учитывать это, мы сможем улучшить нашу модель.
Вывод №1. Попробуйте уменьшить шум в своих данных относительно целевого результата.
Допущения модели
Каждая модель, которую вы используете, содержит допущения. Когда модель оказывается неудачной, бывает полезно выявить и проверить допущения. Первое допущение, которое мы сделали, заключалось в том, что фактическое количество заброшенных шайб является показателем силы и потенциального преимущества команды. Это не лучший подход.
Какие ещё были сделаны допущения, которые стоит пересмотреть?
Поговорим о распределении Пуассона. Нам казалось, что этот метод отлично подходит для наших данных. Но когда мы проанализировали среднее количество заброшенных шайб и значение отклонения, мы пришли к любопытному выводу: средние значения и отклонения для хозяев и гостей оказались разными.
В обоих случаях, вероятно, имел место недостаточный разброс данных. Это может быть серьезной проблемой, поскольку одно из фундаментальных допущений для распределения Пуассона состоит в том, что среднее значение и значение отклонения одинаковы.
Если отклонение превышает среднее значение, лучше использовать отрицательное биномиальное распределение. Если же отклонение меньше среднего значения, лучшим вариантом будет распределение Конвея-Максвелла-Пуассона.
Но при большем размере выборки игр среднее количество заброшенных шайб и значение отклонения может оказаться одинаковым. Так что для наших целей оптимальным выбором может быть другой метод распределения. Важно не останавливаться на каком-либо одном решении, не рассмотрев разные варианты.
Вывод №2. Проверьте допущения модели, распределение и функции.
Неучтенные источники отклонения
Наконец, следует рассмотреть источники отклонения, которые мы не учитывали. Как насчет примеров? Мы исходили из того, что сила команды — величина постоянная. Мы не принимали во внимание травмы ключевых игроков или замены. Может ли, например, "Эдмонтон Ойлерс" играть на одном и том же уровне с Коннором МакДэвидом в составе и без него? Скорее всего, разница в том и другом сценарии будет существенная, и наша модель ее не учитывает.
Кроме того, мы предполагали, что ожидаемое количество заброшенных шайб команды не зависит от того, кто стоит в воротах. Это неверное допущение, потому что основные и запасные вратари имеют разный процент сэйвов. Если учесть все подобные источники отклонений, мы сможем сделать нашу модель более точной.
Следует также учитывать другие факторы, которые наша модель упустила из виду: например, календарь матчей, усталость, судьи, высота над уровнем моря и т. д. Чтобы понимать, на что обращать внимание, нужно обладать знаниями в предметной области. Наша модель не знает, что команда будет играть с запасным вратарем и без двух лидеров, которые травмированы. Но вы-то знаете об этом.
Вывод №3. Используйте свои знания, чтобы находить неучтенные источники отклонений.
Теперь мы понимаем, в чем слабые места нашей модели и как ее улучшить. Мы можем пересмотреть исходные данные, выбрать другой метод распределения и проверить допущения. Секрет успеха заключается в том, чтобы планомерно двигаться вперед, несмотря на неудачи.



